The Pool Game

Introduction

We are given a set of images, each containing

• A pool cue stick with variation in position and orientation.
• A set of balls with numbers which are evenly spaced in vertical direction.

Assuming that the pool cue stick shoots the striker ball in a straight line, and therefore hit at one of the evenly spaced pool balls. The task is to determine which pool ball would the striker ball hit.

Tools

OpenCV 2.4, an Open-source Computer Vision library is used with Python 2.7. For instructions regarding the installation of OpenCV refer documentation.

Task Analysis

From the test images we observe that:

• Diameter of striker ball is less than other pool balls.
• All the other pool balls are of equal diameter = height of image/number of balls.
• Cue stick has two distinct colours not present in any other part of image.

Algorithm

Our goal is to determine the number of pool ball which striker ball would hit. Simply saying, we need to detect the intersection of the line tangent to pool balls and the line which passes through the middle of cue stick and the center of striker ball. The y co-ordinate of intersection will determine the number of target pool ball.

We know from elementary geometry that we require at least two points to construct a line. In this image there are two unique markings on cue stick whose centroid can be used as one of the two points. Also, center of white striker ball can be used as one of the point. I have used center of striker ball and the centroid of pink mark on cue stick to produce a line which can be extrapolated to detect the intersection.

Note: I have assumed upper left corner as origin.

Implementation

• The center of Striker ball

I have used Hough circle transform which is available in OpenCV to detect all the balls. For more information regarding Hough transform, refer this post. This function returns the coordinates of center and radius of all the detected circles. We know that the radius of striker ball will be least. So it is just a matter of traversing the list to find coordinates corresponding to the ball with least radius.

1
2
3
4
5
6
7
8
9
10
11
circles = cv2.HoughCircles(img, cv2.cv.CV_HOUGH_GRADIENT, 1, 20, param1=40, param2=35, minRadius=20, maxRadius=100)
circles = np.uint16(np.around(circles))
rmin = circles[0][0][2]
x = circles[0][0][0]
y = circles[0][0][1]
for i in circles[0, :]:
	# detecting the white ball
	if i[2] < rmin:
		rmin = i[2]
		x = i[0]
		y = i[1]

Tip: Alternatively numpy.argmin() can be used to find the ball with smallest radius.

• Pink patch on cue stick

The coordinates of center of striker ball have already been calculated. Now, another point is required to draw a line. To segment pink patch we will mask the image corrsponding to the color of patch and then use contours to segment out the pink patch from image. For masking first we will convert our image to hsv color space. This is done because it is easier to represent a color in HSV, than in BGR color space. After changing the color space, we threshold the HSV image for pink color. Next, we will find contours in the masked image. As the masked image only contains the pink portion of cue stick, finding contours in this image will return the pik portion of stick as the oly contour. To find the cetroid of this contour, we will use moments method.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
hsv = cv2.cvtColor(img, cv2.COLOR_BGR2HSV)

# masking pink colour in stick
lower_pink = np.array([150, 200, 200])
upper_pink = np.array([200, 255, 255])
mask = cv2.inRange(hsv, lower_pink, upper_pink)

contours, hierarchy = cv2.findContours(mask, cv2.RETR_TREE, cv2.CHAIN_APPROX_NONE)
cnt = contours[0]
cv2.drawContours(img, contours, -1, (255, 0, 0), 1)

# centroid of pink contour
M = cv2.moments(cnt)
cx = int(M['m10']/M['m00'])
cy = int(M['m01']/M['m00'])

Note: To find the HSV values for masking use the below code:

1
2
3
bgr_target = np.uint8([[[255, 0, 0]]])
hsv_target = cv2.cvtColor(bgr_target, cv2.COLOR_BGR2HSV)
print hsv_target

Now take [H-10, 100,100] and [H+10, 255, 255] as lower bound and upper bound respectively.

• Finding the intersection

Till now we have two points using which we can draw a line and extrapolate it to the width of image. Now to detect the point of collision we will need another line which is parallel to the the height of image and is tangent to the pool balls. Now all we require is a point to draw this line. Since the output of the hough transform gives us the coordinates of center and radius of other pool balls, we can subtract the radius of ball from the x coordinate of center to find a point passing through the second line. Now the only part left is detecting the intersection of these two lines. Refer this post to read on how to detect intersecting lines. Since all the pool balls are evenly stacked and the number on the balls is same in all the test images, the y coordinate of the point of intersection of above lines will determine the ball which was hit.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
s10_x = p1[0] - p0[0]
s10_y = p1[1] - p0[1]
s32_x = p3[0] - p2[0]
s32_y = p3[1] - p2[1]

denom = s10_x * s32_y - s32_x * s10_y
if denom == 0:
	return None  # collinear

denom_is_positive = denom > 0

s02_x = p0[0] - p2[0]
s02_y = p0[1] - p2[1]

s_numer = s10_x * s02_y - s10_y * s02_x
if (s_numer < 0) == denom_is_positive:
	return None  # no collision

t_numer = s32_x * s02_y - s32_y * s02_x
if (t_numer < 0) == denom_is_positive:
	return None  # no collision

if (s_numer > denom) == denom_is_positive or (t_numer > denom) == denom_is_positive:
	return None  # no collision

# collision detected
t = float(t_numer) / denom
intersection_point = [int(round(p0[0] + (t * s10_x))), int(round(p0[1] + (t * s10_y)))]

Results

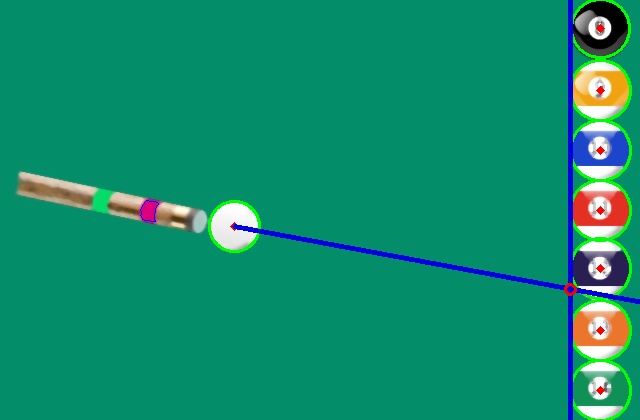
Refer my repository for complete code.

Thanks!