Maze Solver

Introduction

This project aims at finding the solution of perfect mazes which is defined as a maze which has only one path from any point in the maze to any other point. Also, maze has no inaccessibe sections, no circular paths and no open areas. Maze images should have dark walls on light background. I have included some sample images. To generate mazes, this online maze generator can be used. This project idea is taken from this File exchange submission.

Tools

OpenCV 2.4, an Open-source Computer Vision library is used with Python 2.7. For instructions regarding the installation of OpenCV refer documentation.

Task Analysis

Perfect mazes have a characteristic that their is only one possible path from start to end. This means that this image can be divided into two parts and this boundary of division will be the solution itself. Therefore, morphological transformatons like erosion and dilation are just enough to find the solution of the maze.

Dilation

Dilation is one of the two basic operators in the area of mathematical morphology, the other being erosion. It is typically applied to binary images, but there are versions that work on grayscale images. The basic effect of the operator on a binary image is to gradually enlarge the boundaries of regions of foreground pixels (i.e. white pixels, typically). Thus areas of foreground pixels grow in size while holes within those regions become smaller.

Erosion

Erosion is the second morphological operator. It is also applied to binary images. The basic effect of the operator on a binary image is to erode away the boundaries of regions of foreground pixels (i.e. white pixels, typically). Thus areas of foreground pixels shrink in size, and holes within those areas become larger.

Implementation

• Load and convert the source image to binary image

1
2
3
img = cv2.imread('maze.png')
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
ret, thresh = cv2.threshold(gray, 127, 255, cv2.THRESH_BINARY_INV)

Inverted thresolding will give us a binary image with white wall and black background.

• Find the contours

1
2
3
contours, hierarchy = cv2.findContours(thresh, cv2.RETR_EXTERNAL, cv2.CHAIN_APPROX_NONE)
cv2.drawContours(thresh, contours, 0, (255, 255, 255), -1)
ret, thresh = cv2.threshold(thresh, 240, 255, cv2.THRESH_BINARY)

Since, the maze can be divided into an open path seperated by two walls, finding contours will give us both the walls. Select ay contour for further operations.

• Dilate the contour

1
2
kernel = np.ones((19, 19), np.uint8)
dilation = cv2.dilate(thresh, kernel, iterations=1)

• Erode the Dilated image by same amount

1
2
kernel = np.ones((19, 19), np.uint8)
erosion = cv2.erode(dilation, kernel, iterations=1)

• Find diff of two images

1
diff = cv2.absdiff(dilation,erosion)

The absolute difference of two images will give us the solution of maze.

• Draw the obtained path on source images

1
2
3
4
5
6
7
8
b, g, r = cv2.split(img)
mask_inv = cv2.bitwise_not(diff)

# masking out the green and red colour from the solved path
r = cv2.bitwise_and(r, r, mask=mask_inv)
g = cv2.bitwise_and(g, g, mask=mask_inv)

res = cv2.merge((b, g, r))

To show the solution on the original maze image, first split the original maze into it’s r, g, b components. Now create a mask by inverting the diff image. Bitwise and r and g components of original maze using the mask created in the last step. This step would remove the red and green components from the portion of image where solution of maze exists. The last is to merge all the components and we will have the final image with solution marked by blue colour.

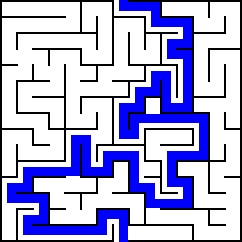
Refer my repository for complete C++ and Python implementation.

Thanks!